Probability distribution of multiplied dice rolls
While playing D&D, I wondered: Is there any difference between rolling 1d8×2 (that is, rolling exactly one d8 and multiplying the result by 2) and rolling 2d8 (that is, rolling exactly two d8s and not modifying the result)?
(For those who don’t know, a d8 is an eight-sided die. A six-sided die is a d6; the 20-sided die is the d20; and so on. In D&D, the d20 is used to check whether something succeeds, and other dice such as d4s, d6s, d8s, and d10s are used to measure damage dealt or occasionally to pick a random one of a small pool of (possibly unknown) choices.)
The intuitive answer is no, they’re equivalent. As is typical in statistics and probability, the intuitive answer is wrong.
I wrote a Python script to simulate 10,000 dice rolls, store the natural results of those rolls for later measurement, and then use them to graph out the results of as many of the requested roll as possible. You tell it something like “1d8x2”, “2d8”, or “1d8x2+4”, and it prints out a histogram of how many times each total result came up.
With 1d8, the distribution tends toward uniform (I used Python’s `random.choice`, which is based on `random.uniform`):
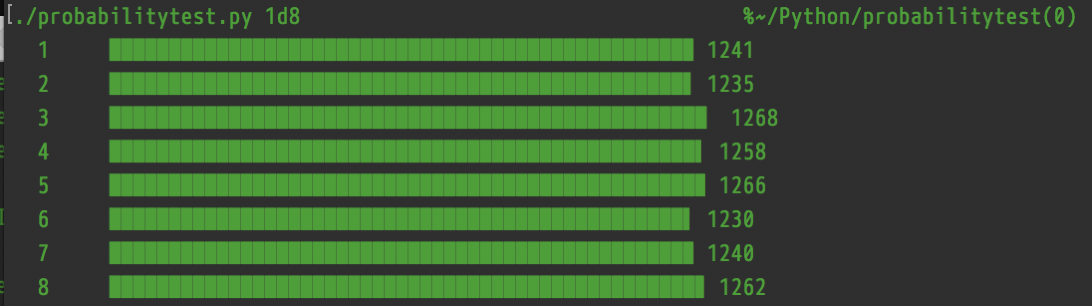
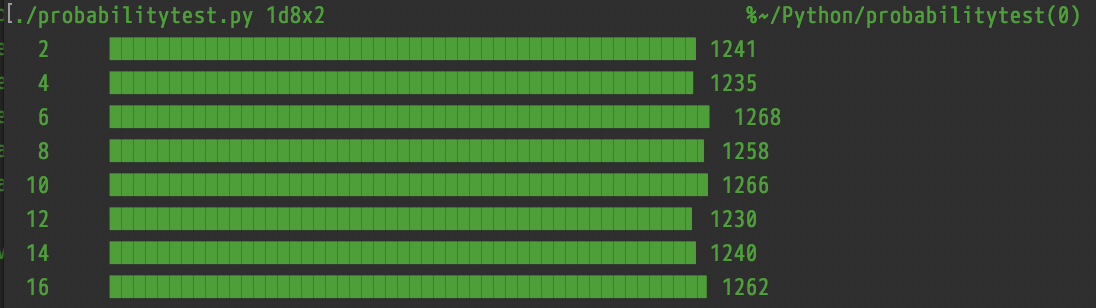
1d8×2 uses exactly the same rolls and simply multiplies the total of the natural rolls, so it produces exactly the same histogram, except distributed over 2–16 (stepping by 2) instead of 1–8:
2d8, however, changes the distribution dramatically:
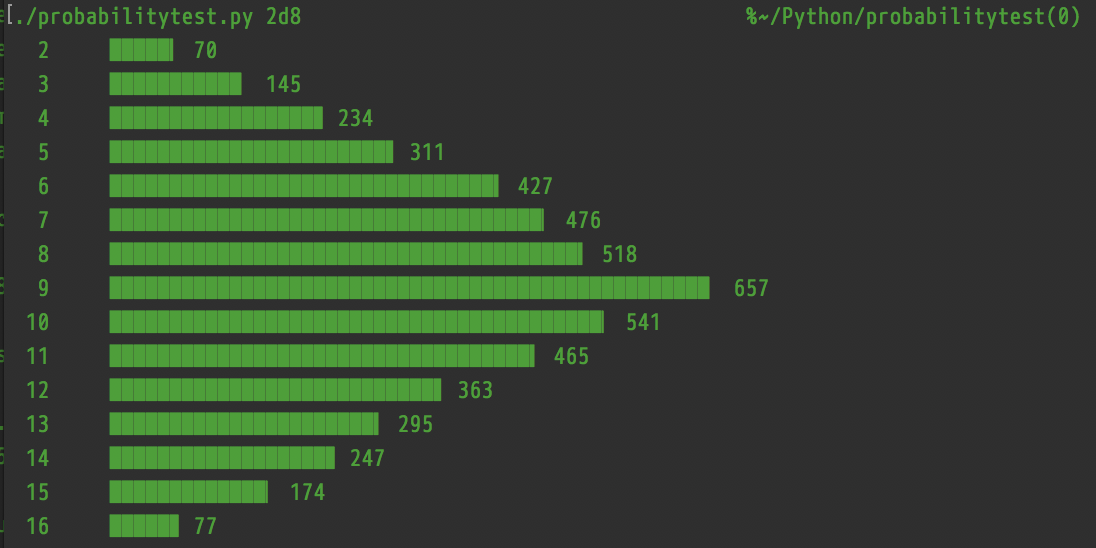
If this is a damage roll (the moment that inspired this experiment was when I landed a critical hit), 1d8x2 means you’re equally likely to do any amount of damage, including both the minimum and the maximum, whereas 2d8 not only doubles the range (from 1–8 to 2–16), it also makes the lower end of that range much less likely, and makes the high end of the original range (the middle of the new range) the most likely.
There is another aspect to the question of whether to double the result or roll the dice twice, and that’s what does the Player’s Handbook (or equivalent if you’re playing something other than D&D) say?
The D&D 5.0 Player’s Handbook says:
When you score a critical hit, you get to roll extra dice for the attack’s damage against the target. Roll all of the attack’s damage dice twice and add them together. Then add any relevant modifiers as normal. To speed up play, you can roll all the damage dice at once.
For example, if you score a critical hit with a dagger, roll 2d4 for the damage, rather than 1d4, and then add your relevant ability modifier. If the attack involves other damage dice, such as from the rogue’s Sneak Attack feature, you roll those dice twice as well.
So the 5e Player’s Handbook makes crystal-clear that, in the circumstance that inspired this experiment, 2d8 is the correct roll. Fortunately, that’s what I did—but now I can be more certain of that going forward, partly because now I understand why.